In this article, we are going to learn about Triangle congruence theorems, Similar Triangles, and Relationships between the Sides of a Triangle.
A pair of triangles are congruent if their side lengths are the same and their angles are the same size.
SAS Congruence Theorem
Two triangles are congruent if two sets of their sides are the same length and their angles are equal in measurement.
ASA Congruence Theorem
A triangle is congruent if two angles are of equal measurement and if the sides of the triangles are all the same length.
SSS Congruence Theorem
Two triangles are congruent if three pairs of sides are equal in length.
SSA Congruence Theorem
SSA does not always prove congruence if two sides are opposite at equal angles. Angles are not included in the condition even if they are opposite equal sides.
Note
Triangle congruence theorems is proved by the SSA condition for an obtuse angle or a right angle. If the angle is right (also called the HL condition or the RHS condition), we can calculate the Third Side and apply SSS.
For acute angles, SSA does not make congruence when the opposite side is shorter than the known adjacent side, but longer than the sine of the angle times the adjacent side. In all other cases, SSA makes the congruence with the corresponding equalities.
AAA Congruence Theorem
In this case, AAA (Angle*Angle*Angle) proves only similarity and not congruence since it does not indicate the size of the two triangles.
How to prove triangles are similar
- To conclude that two triangles are similar, only two sets of angles need to be the same; the third will be identical since all angles of a triangle sum to 180.
- Triangles with similar sides have the same angle measures as triangles with similar sides. For instance, a triangle with lengths 3, 4, and 5 has the same angle measures as a triangle with lengths 6, 8, and 10. Each triangle is similar, and the smaller triangle has legs twice as long as the larger triangle.
- The ratio of the sides of two similar triangles is X/y, and they have the same area as X2/y2.
Relationship of the Sides of a Triangle
Generally, each of the three sides of a triangle should be larger than the positive difference between the other two sides, but smaller than their sums.
What are Consecutive Interior Angles
- Triangles are constructed using two interior angles that add to 180°.
- Each interior angle must be less than 180° because the angles add to 180°.
- The bisectors of the three interior angles converge at the incenter, which is the center of the triangle.
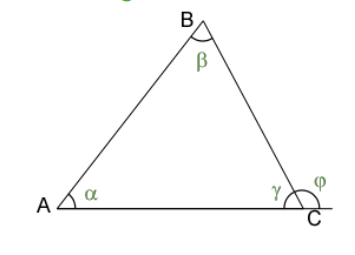
How to Find Exterior Angles of a Triangle
- The angle between the extension of one side of a triangle and its side is known as the exterior angle.
- In a triangle, the exterior angle is equal to the sum of the opposite interior angles.
- The exterior angles of any convex polygon always add up to 360°, regardless of its vertex. This holds for each vertex for any convex polygon, not just triangles.
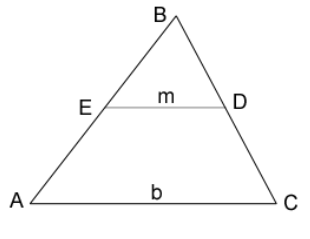
How to find Midsegment of a Triangle
- An angle between the midpoints of two sides of a triangle is called a midsegment
- Triangles have three possible midpoints.
- The midpoint of a triangle will always be parallel to the third side.
- It will give half the length of the third side.
- A triangle will have three possible midpoints, depending on which pair of sides leads to the midpoint.
Take Away: If you find Triangle congruence theorems helpful, you may also be interested in reading the following advanced level articles on triangles
- Properties of the incenter of a triangle and circumcenter of a triangle
